激活函数

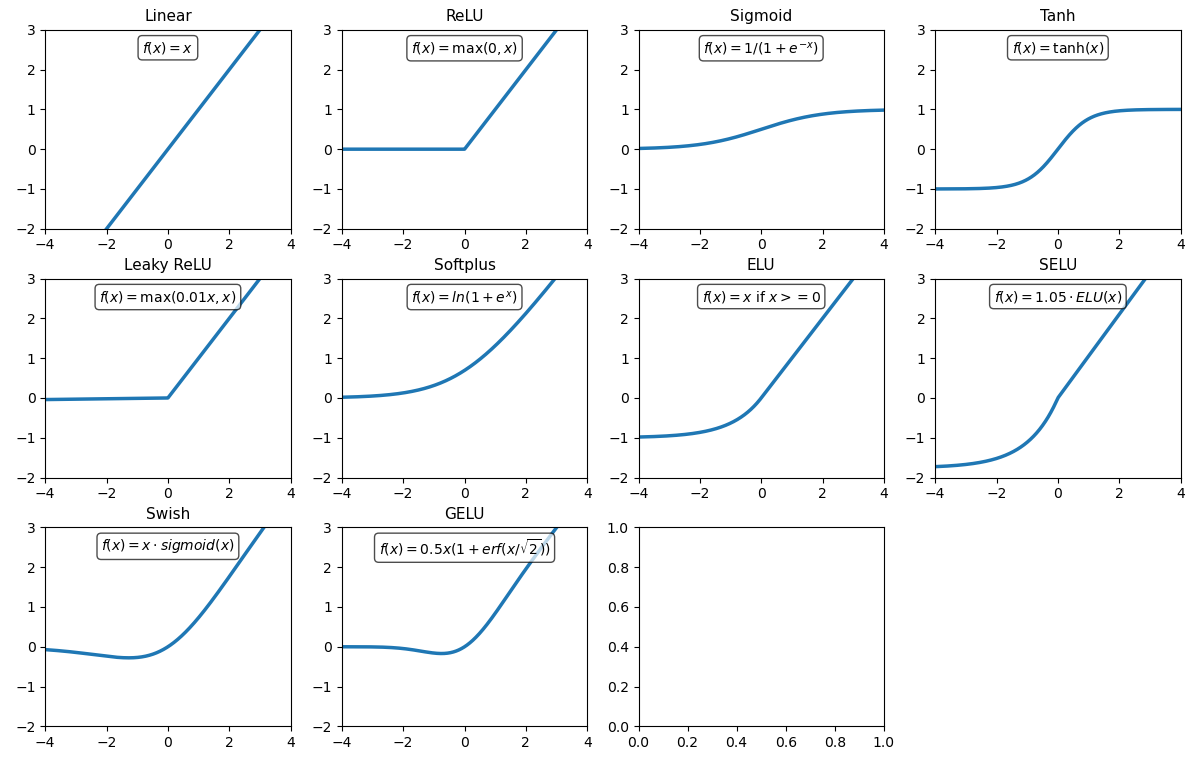
Linear Activation

$f(x) = x$

ReLU

$f(x) = \max(0,\, x)$

隐藏层中最常用，计算高效，缓解梯度消失

Sigmoid

$f(x) = \frac{1}{1+\mathrm{e}^{-x}}$

二分类输出层，输出概率值

Tanh

$f(x) = \tanh(x) = \frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}}$

RNN 隐藏层，输出范围 [-1, 1]，零中心化

Leaky ReLU

f(x) = \begin{cases} x, & x\ge 0\\[4pt] \alpha x, & x<0 \end{cases} \quad (\alpha\in(0,1))

深层网络中替代 ReLU，提升训练稳定性

Softplus

$f(x) = \ln\!\bigl(1+\mathrm{e}^{x}\bigr)$

ReLU 的平滑近似，用于需要平滑激活的场景，如概率模型

ELU

f(x)= \begin{cases} x, & x\ge 0\\[4pt] \alpha\,(\mathrm{e}^{x}-1), & x<0 \end{cases}

加速收敛，输出均值接近 0，适合深层网络

SELU

f(x)=\lambda \begin{cases} x, & x\ge 0\\[4pt] \alpha\,(\mathrm{e}^{x}-1), & x<0 \end{cases}

类似 ELU，但斜率更大，自归一化网络中，保持层间分布稳定
其中 $\lambda\approx 1.050\ 7$，$\alpha\approx 1.673\ 3$。

Swish

f(x)=x\cdot\sigma(\beta x)=x\cdot\frac{1}{1+\mathrm{e}^{-\beta x}} \quad (\beta=1 时称为 SiLU)

深度模型中性能优于 ReLU，如 EfficientNet

GELU

$f(x)=x\cdot\Phi(x)=\frac{x}{2}\left[1+\mathrm{erf}\!\left(\frac{x}{\sqrt{2}}\right)\right]$

类似 Swish，但更平滑，Transformer、BERT、GPT 等模型中广泛使用

激活函数	非线性	输出范围	常用于	特点
Linear	否	(-∞, ∞)	回归输出	简单
ReLU	是	[0, ∞)	隐藏层	快速、稀疏
Sigmoid	是	(0, 1)	二分类输出	易饱和
Tanh	是	(-1, 1)	RNN	零中心化
LeakyReLU	是	(-∞, ∞)	隐藏层	解决死神经元
Softplus	是	(0, ∞)	平滑 ReLU	可导
ELU	是	(-α, ∞)	深层网络	加速收敛
SELU	是	类似 ELU	自归一化网络	自动归一化
Swish	是	(-∞, ∞)	深层模型	非单调
GELU	是	(-∞, ∞)	Transformer	高斯加权